
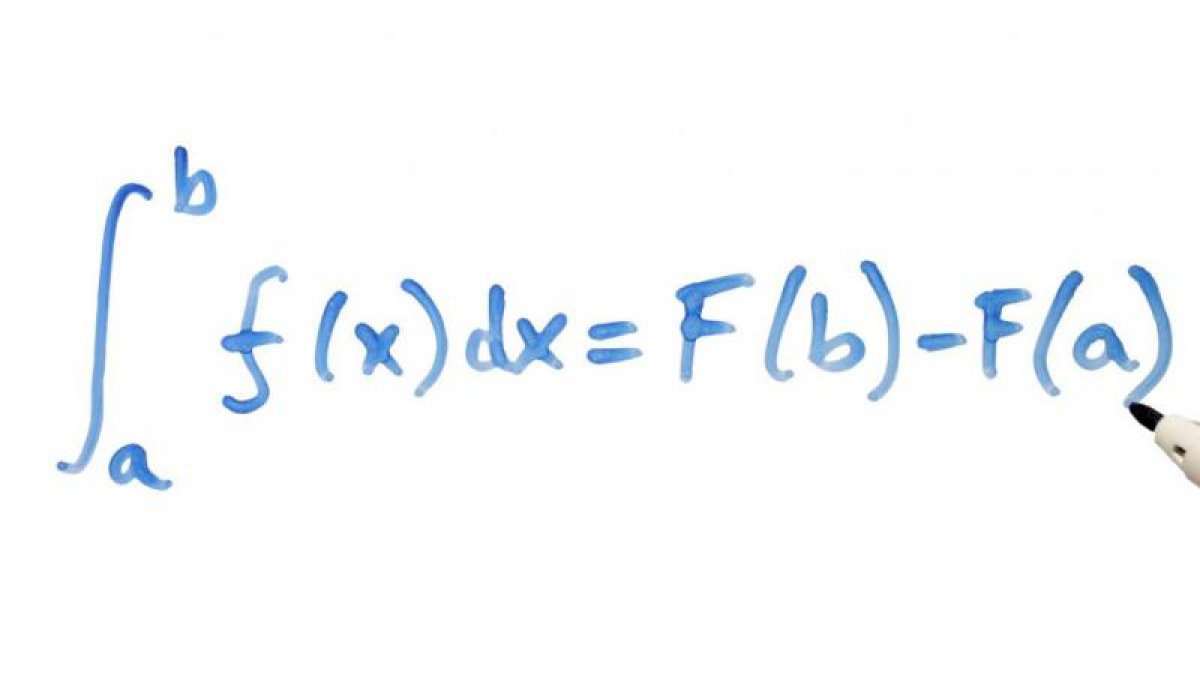
Also the inverse trigonometric functions will be covered quicky in Calculus II. Trigonometric identities will be used extensively in calculus II. Section 4.4: Exponential and Logarithmic Equations. The following sections will be very useful for your preparation. It would be wise to practice using the laws of logarithms and exponents etc. Logarithmic and Exponential functions will be introduced and used throughout Calculus II.

Section 2.8: One-to-One Functions and Their Inverses.Ĭhapter 4: Exponential and Loarithmic Functions.

For an introductory approach to One-to-One Functions and Their Inverse, please read: Section 2.8 will be covered briefly in calculus II, in addition to the relationship between derivatives of functions and derivatives of their inverses ( when derivatives and inverses exist). We plan to add videos to this webpage in the future. You may also find information on these topics on the internet including videos on Khan Academy.

It is available on both new and second hand at very reasonable prices. If you do not have access to a precalculus book, it is strongly suggested that you obtain a copy of this book for reference throughout the calculus sequence. Precalculus, Fifth Edition, by Stewart, Redlin, Watson. The suggestestions given below are based on the following book: What does its value represent? It represents the rate of change of F around that point x and naturally it means it is the derivative of the integral F.There are many topics from precalculus used in this course and you may need to refresh your memory on these topics. On a diagram, there's a yellow line with an x label. If you're struggling to get a good grasp on this fundamental concept try this: check out this video - and consider the following: it is a very subtle and simple idea: You don't differentiate the f(t) because it is in fact your original function before integration.įundamental Theorem of Calculus is tricky to understand but once you know it by heart it'll never leave you. Now, if you take the derivative of this integral you get f(x^4) times d/dx(x^4). The definite integral equals F(x)=Integral(f(t)) from 0 to x^4. Your conclusions are alright but you're not solving for what's being asked.


 0 kommentar(er)
0 kommentar(er)
